
科目:gzsx 來源: 題型:
科目:gzsx 來源:2012-2013學年江西省南昌二中高二(上)期中數(shù)學試卷(文科)(解析版) 題型:選擇題




科目:gzsx 來源:2012-2013學年江西省南昌二中高二(上)期中數(shù)學試卷(理科)(解析版) 題型:選擇題




科目:gzsx 來源:2012-2013學年江西省南昌二中高二(上)期中數(shù)學試卷(文科)(解析版) 題型:選擇題
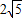
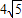
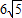
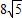
科目:gzsx 來源:2012-2013學年江西省南昌二中高二(上)期中數(shù)學試卷(理科)(解析版) 題型:選擇題
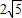
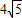
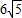
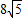
科目:gzsx 來源: 題型:
科目:gzsx 來源: 題型:
科目:gzsx 來源: 題型:
| 2 |
科目:gzsx 來源: 題型:
科目:gzsx 來源: 題型:
科目:gzsx 來源: 題型:
科目:gzsx 來源: 題型:
| 5 |
科目:gzsx 來源: 題型:
科目:gzsx 來源: 題型:
科目:gzsx 來源: 題型:
科目:gzsx 來源: 題型:
科目:gzsx 來源: 題型:
科目:gzsx 來源: 題型: